Bayesian Model Comparison

Contents

22. Bayesian Model Comparison#

What alternatives do we have for AIC and BIC when we don’t have a maximum Liklihood?

import numpy as np
import pymc as pm
import arviz as az
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_theme(context="talk", style="ticks", font="serif", color_codes=True)

np.random.seed(0)

c_true = (5, 0.12, 11/4)
N = 50
x = np.sort(10*np.random.rand(N))
yerr = 1 + 5 * np.random.rand(N)
y = c_true[0] + c_true[1]*x + c_true[2]*x**2
y += yerr * np.random.randn(N)

plt.errorbar(x, y, yerr=yerr, fmt="k.");

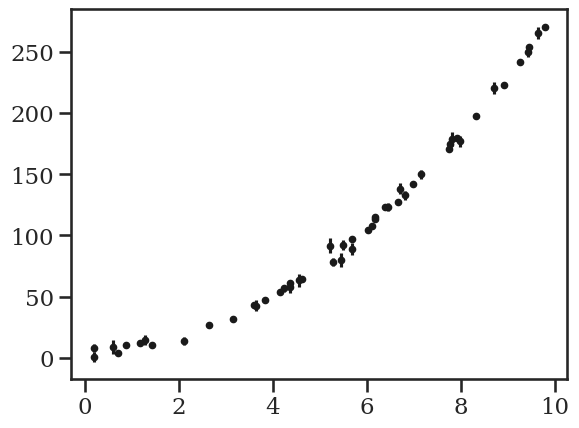
../../_images/46c559ef854d7b67b632185002ce8d02a11e6bd8a4d04cbc0beb9d41f41544ea.png

# model is y = c0 + c1*x + c2*x^2 + noise

# build a model via a `with` context block.
with pm.Model() as model:
    # define priors on polynomial coeffiencts and the added noise
    c0 = pm.Normal('c0', 0, 20)
    c1 = pm.Normal('c1', 0, 20)
    c2 = pm.Normal('c2', 0, 20)
    noise = pm.Exponential('noise', 0.1) #could be half-Normal or half-chauchy

    # define observations: y = c0 + c1*x + c2*x^2
    # link variables to data with `observed=y`
    obs = pm.Normal('obs', c0 + c1*x + c2*x**2, noise, observed=y)

    # run sampler
    idata_quad = pm.sample(idata_kwargs={"log_likelihood": True})

idata_quad

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [c0, c1, c2, noise]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.

arviz.InferenceData

# model is y = c0 + c1*x  + noise

# build a model via a `with` context block.
with pm.Model() as model:
    # define priors on polynomial coeffiencts and the added noise
    c0 = pm.Normal('c0', 0, 20)
    c1 = pm.Normal('c1', 0, 20)
    noise = pm.Exponential('noise', 0.1) #could be half-Normal or half-chauchy

    # define observations: y = c0 + c1*x + c2*x^2
    # link variables to data with `observed=y`
    obs = pm.Normal('obs', c0 + c1*x, noise, observed=y)

    # run sampler
    idata_linear = pm.sample(idata_kwargs={"log_likelihood": True})

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [c0, c1, noise]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.

# model is y = c0 + c1*x + c2*x^2 + c3*x^3  + noise

# build a model via a `with` context block.
with pm.Model() as model:
    # define priors on polynomial coeffiencts and the added noise
    c0 = pm.Normal('c0', 0, 20)
    c1 = pm.Normal('c1', 0, 20)
    c2 = pm.Normal('c2', 0, 20)
    c3 = pm.Normal('c3', 0, 20)
    noise = pm.Exponential('noise', 0.1) #could be half-Normal or half-chauchy

    # define observations: y = c0 + c1*x + c2*x^2 + c3*x^3
    # link variables to data with `observed=y`
    obs = pm.Normal('obs', c0 + c1*x + c2*x**2 + c3*x**3, noise, observed=y)

    # run sampler
    idata_cubic = pm.sample(idata_kwargs={"log_likelihood": True})

Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [c0, c1, c2, c3, noise]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 5 seconds.
There were 2 divergences after tuning. Increase `target_accept` or reparameterize.

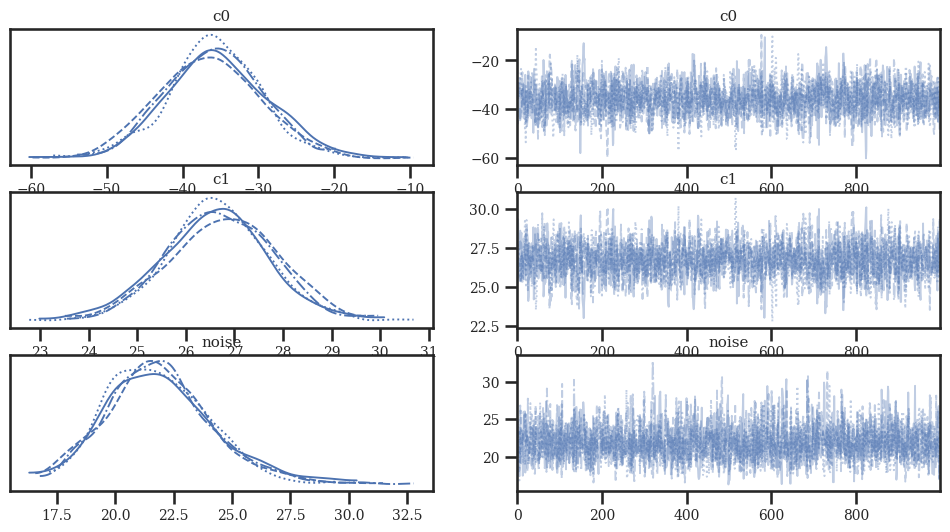
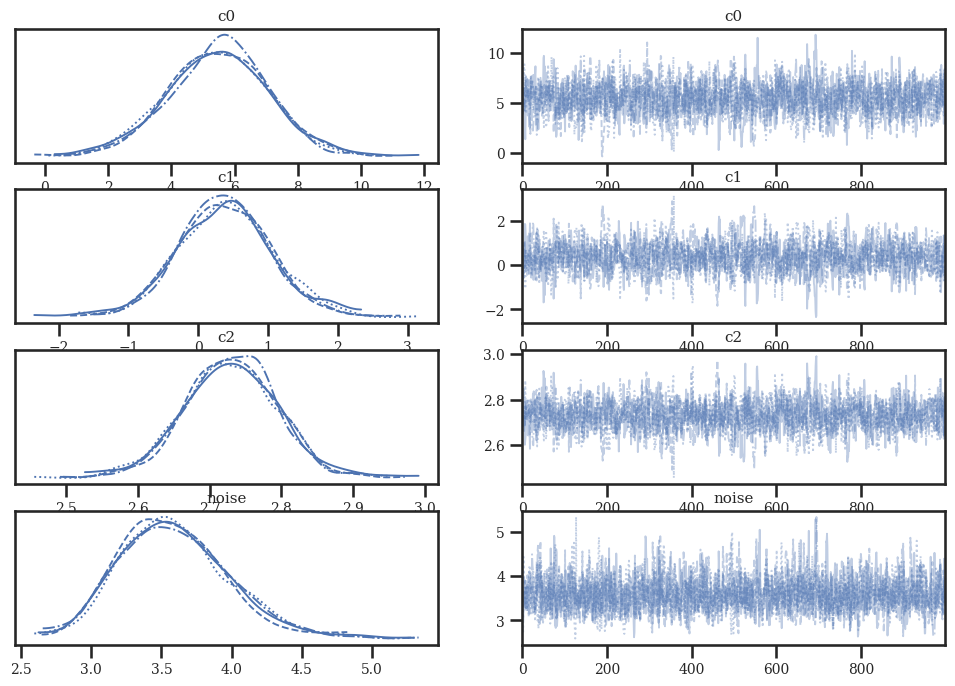
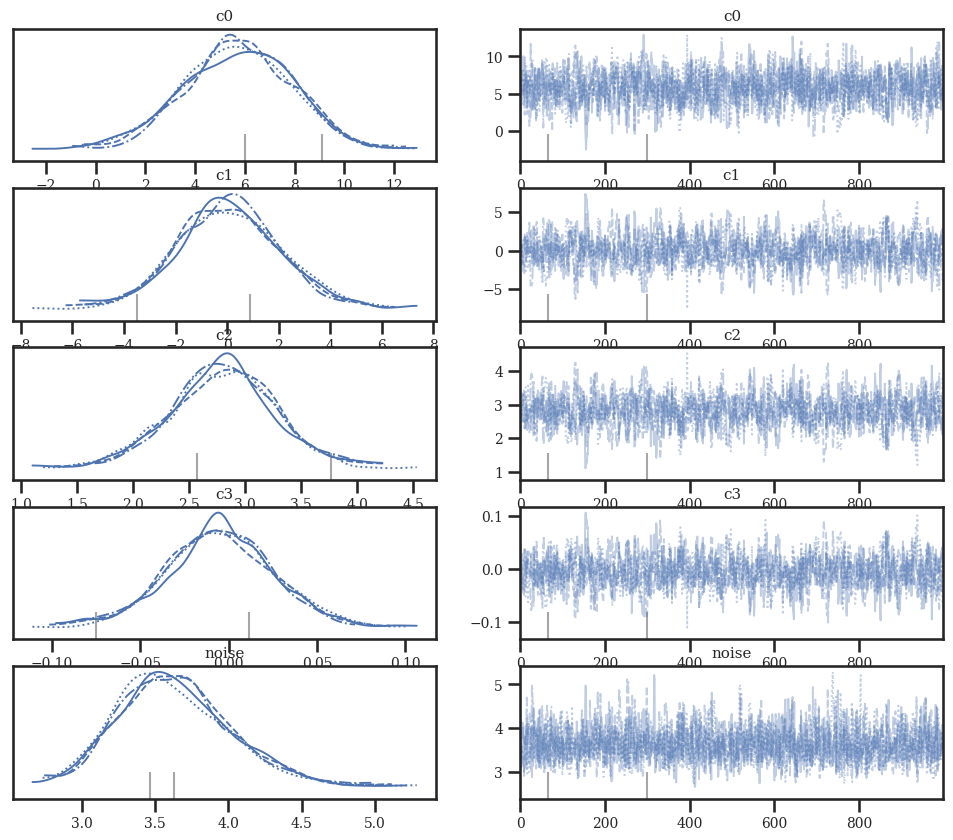
az.plot_trace(idata_linear)
az.plot_trace(idata_quad)
az.plot_trace(idata_cubic);

../../_images/79bc26d9ea31620b96d94d144cb5c0f9a9e7742ef9e00b6bc586b34dc140777c.png

../../_images/b5324064b09280081f0aedfc5e082097c9a8b7a7f8b02bc835c2c935a443f1ba.png

../../_images/ab0adfbe49496b1f05d2e6414b2b55e5f4992692da44e3156f09cca6b14df4d0.png

22.1. Cross Valication & Leave-one-out#

Gelman, Hill, & Vehtari section 11.8 describes the theory behind the following process

https://python.arviz.org/en/stable/api/generated/arviz.compare.html https://python.arviz.org/en/latest/api/generated/arviz.plot_compare.html

Note, you need idata_kwargs={"log_likelihood": True} in the pm.sample() function in order to save the likelihoods needed for the fast leave-one-out calcualtions described in Gelman 11.8.

# Perform the Leave-one-out calcualtion
idata_linear = az.loo(idata_linear)
idata_quad = az.loo(idata_quad)
idata_cubic = az.loo(idata_cubic)

model_compare = az.compare(
    {
        "linear": idata_linear,
        "quad": idata_quad,
        "cubic": idata_cubic,
    }
)
az.plot_compare(model_compare, figsize=(11.5, 5));

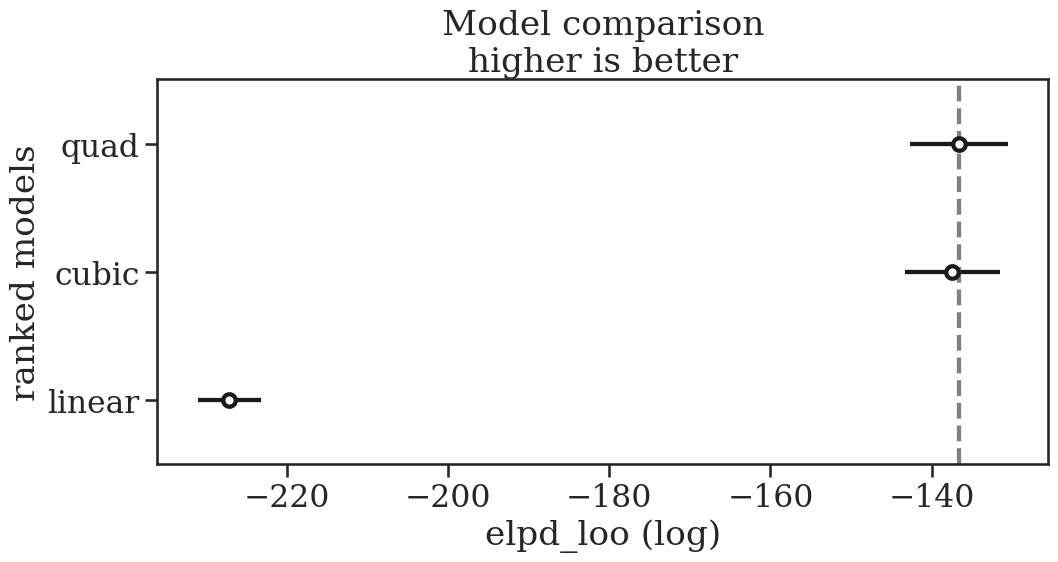
../../_images/ba58f2801f0ab4818fac2208694effaa6bffab02e266c98209de1f200d6eef8e.png

# Lets zoom in on quad and cubic
model_compare = az.compare(
    {
        "quad": idata_quad,
        "cubic": idata_cubic,
    }
)
az.plot_compare(model_compare, figsize=(11.5, 5), insample_dev=True);

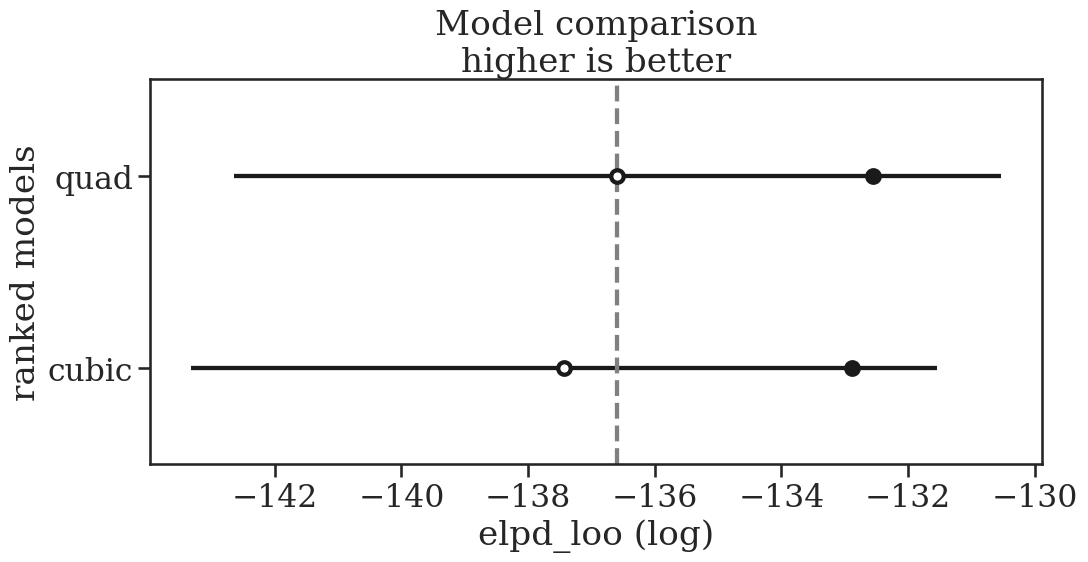
../../_images/c29a54bcce0b8ccba38c58a94c779d5dafc8aebce04fa3b2c8117a4d3f63722d.png

22.2. Further Reading#

%load_ext watermark
%watermark -untzvm -iv -w

Last updated: Wed Apr 23 2025 13:53:53CDT

Python implementation: CPython
Python version       : 3.11.12
IPython version      : 9.1.0

Compiler    : Clang 18.1.8 
OS          : Darwin
Release     : 24.4.0
Machine     : arm64
Processor   : arm
CPU cores   : 12
Architecture: 64bit

pandas    : 2.2.3
numpy     : 1.25.2
rich      : 14.0.0
pymc      : 5.22.0
seaborn   : 0.13.2
matplotlib: 3.10.1
arviz     : 0.21.0

Watermark: 2.5.0