20. emcee and Bayesian Software Tools#
20.1. Review of emcee#
import emcee
import numpy as np
import matplotlib.pyplot as plt
c_true = (5, 0.12, 11/4)
N = 50
x = np.sort(10*np.random.rand(N))
yerr = 1 + 5 * np.random.rand(N)
y = c_true[0] + c_true[1]*x + c_true[2]*x**2
y += yerr * np.random.randn(N)
plt.errorbar(x, y, yerr=yerr, fmt="k.");
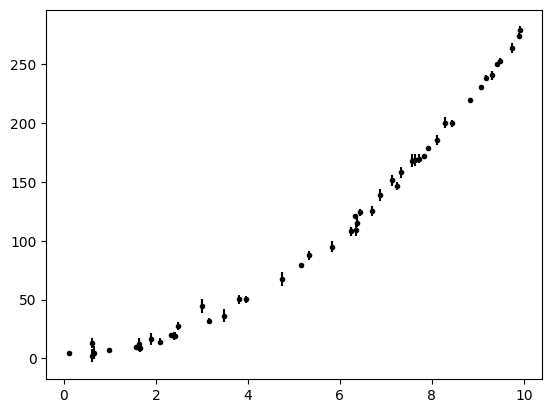
def log_likelihood(theta, x, y, yerr):
theory = theta[0] + theta[1] * x + theta[2] * x**2
return -0.5 * np.sum((y-theory) **2 / yerr**2 + np.log(yerr))
def log_prior(theta):
if -10 < theta[0] < 10 and -10 < theta[1] < 10 and -10 < theta[2] < 10:
return 0.0
return - np.inf
def log_prob(theta, x, y, err):
lp = log_prior(theta)
if not np.isfinite(lp):
return -np.inf
return lp + log_likelihood(theta, x, y, yerr)
nwalkers, ndim = 32, 3
pos = [0, 0, 0] + 1e-3 * np.random.randn(nwalkers, ndim)
sampler = emcee.EnsembleSampler(nwalkers, ndim, log_prob, args=(x, y, yerr))
sampler.run_mcmc(pos, 5000, progress=True);
100%|██████████████████████████████████████████████████████████████████████████████| 5000/5000 [00:01<00:00, 2749.87it/s]
20.2. Arviz: Exploratory analysis of Bayesian models#
https://python.arviz.org/en/latest/index.html
import arviz as az
idata = az.from_emcee(sampler, var_names=["c0", "c1", "c2"])
idata
arviz.InferenceData
-
<xarray.Dataset> Size: 4MB Dimensions: (chain: 32, draw: 5000) Coordinates: * chain (chain) int64 256B 0 1 2 3 4 5 6 7 8 ... 23 24 25 26 27 28 29 30 31 * draw (draw) int64 40kB 0 1 2 3 4 5 6 ... 4994 4995 4996 4997 4998 4999 Data variables: c0 (chain, draw) float64 1MB -0.001906 -0.00144 ... 4.517 4.517 c1 (chain, draw) float64 1MB -9.9e-06 -0.0004835 ... 0.667 0.667 c2 (chain, draw) float64 1MB -4.021e-05 7.8e-05 ... 2.688 2.688 Attributes: created_at: 2025-04-17T16:36:19.437277+00:00 arviz_version: 0.21.0 inference_library: emcee inference_library_version: 3.1.6 -
<xarray.Dataset> Size: 1MB Dimensions: (chain: 32, draw: 5000) Coordinates: * chain (chain) int64 256B 0 1 2 3 4 5 6 7 8 ... 23 24 25 26 27 28 29 30 31 * draw (draw) int64 40kB 0 1 2 3 4 5 6 ... 4994 4995 4996 4997 4998 4999 Data variables: lp (chain, draw) float64 1MB -9.589e+04 -9.589e+04 ... -54.32 -54.32 Attributes: created_at: 2025-04-17T16:36:19.434974+00:00 arviz_version: 0.21.0 inference_library: emcee inference_library_version: 3.1.6 -
<xarray.Dataset> Size: 2kB Dimensions: (arg_0_dim_0: 50, arg_1_dim_0: 50, arg_2_dim_0: 50) Coordinates: * arg_0_dim_0 (arg_0_dim_0) int64 400B 0 1 2 3 4 5 6 ... 43 44 45 46 47 48 49 * arg_1_dim_0 (arg_1_dim_0) int64 400B 0 1 2 3 4 5 6 ... 43 44 45 46 47 48 49 * arg_2_dim_0 (arg_2_dim_0) int64 400B 0 1 2 3 4 5 6 ... 43 44 45 46 47 48 49 Data variables: arg_0 (arg_0_dim_0) float64 400B 0.1032 0.608 0.6202 ... 9.892 9.906 arg_1 (arg_1_dim_0) float64 400B 4.933 2.136 13.14 ... 274.4 279.4 arg_2 (arg_2_dim_0) float64 400B 1.674 5.671 4.402 ... 2.336 2.816 Attributes: created_at: 2025-04-17T16:36:19.436114+00:00 arviz_version: 0.21.0 inference_library: emcee inference_library_version: 3.1.6
az.plot_posterior(idata, var_names=["c0", "c1", "c2"]);
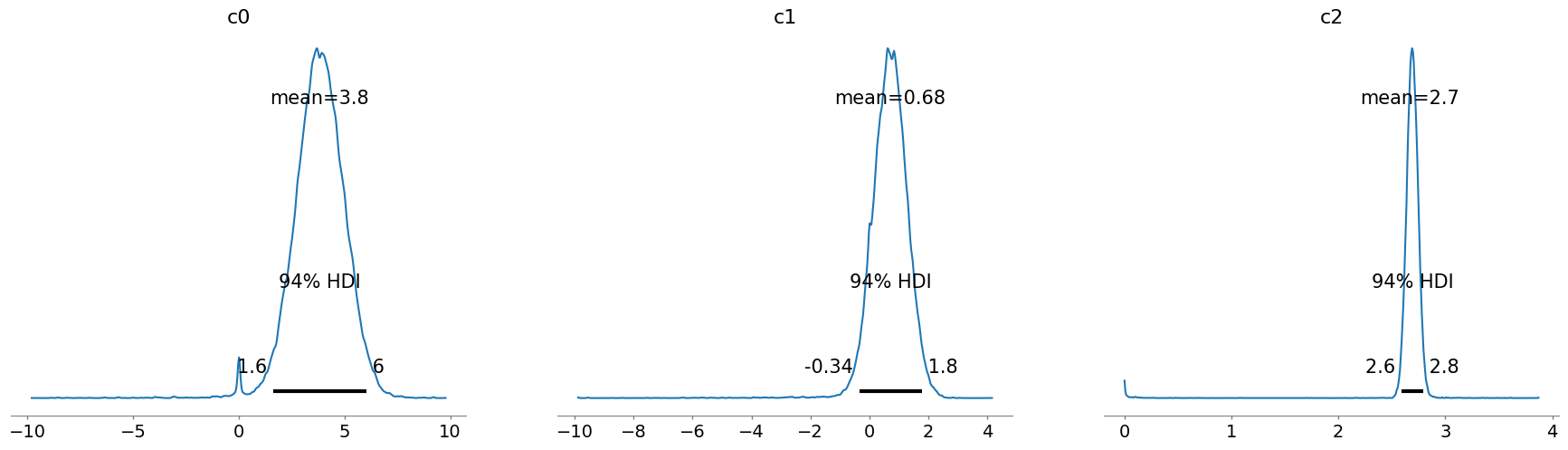
az.plot_trace(idata, var_names=("c0", "c2"));
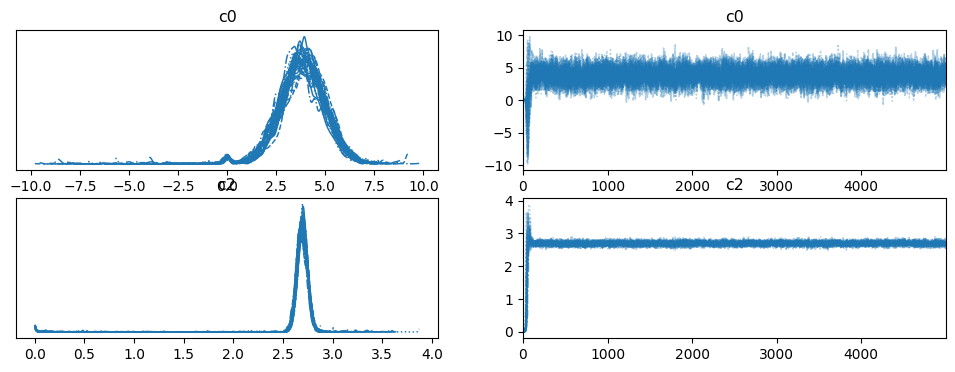
20.3. blobs: unlock sample stats, posterior predictive and miscellanea#
We will see how to do this first with emcee, but define these terms with pymce.
def log_prob_blobs(theta, x, y, err):
lp = log_prior(theta)
like_vector = log_likelihood(theta, x, y, yerr)
like = np.sum(like_vector)
return lp + like, like_vector
sampler = emcee.EnsembleSampler(nwalkers, ndim, log_prob_blobs, args=(x, y, yerr))
sampler.run_mcmc(pos, 5000, progress=True);
100%|██████████████████████████████████████████████████████████████████████████████| 5000/5000 [00:02<00:00, 2238.72it/s]
idata = az.from_emcee(
sampler,
var_names=["c0", "c1", "c2"],
blob_names=["log_likelihood"],
)
idata
arviz.InferenceData
-
<xarray.Dataset> Size: 4MB Dimensions: (chain: 32, draw: 5000) Coordinates: * chain (chain) int64 256B 0 1 2 3 4 5 6 7 8 ... 23 24 25 26 27 28 29 30 31 * draw (draw) int64 40kB 0 1 2 3 4 5 6 ... 4994 4995 4996 4997 4998 4999 Data variables: c0 (chain, draw) float64 1MB -0.001906 -0.00144 ... 4.517 4.517 c1 (chain, draw) float64 1MB -9.9e-06 -0.0004835 ... 0.667 0.667 c2 (chain, draw) float64 1MB -4.021e-05 7.8e-05 ... 2.688 2.688 Attributes: created_at: 2025-04-17T16:36:22.411418+00:00 arviz_version: 0.21.0 inference_library: emcee inference_library_version: 3.1.6 -
<xarray.Dataset> Size: 1MB Dimensions: (chain: 32, draw: 5000, log_likelihood_dim_0: 1) Coordinates: * chain (chain) int64 256B 0 1 2 3 4 5 6 ... 26 27 28 29 30 31 * draw (draw) int64 40kB 0 1 2 3 4 ... 4996 4997 4998 4999 * log_likelihood_dim_0 (log_likelihood_dim_0) int64 8B 0 Data variables: log_likelihood (chain, draw, log_likelihood_dim_0) float64 1MB -9.... Attributes: created_at: 2025-04-17T16:36:22.408267+00:00 arviz_version: 0.21.0 inference_library: emcee inference_library_version: 3.1.6 -
<xarray.Dataset> Size: 1MB Dimensions: (chain: 32, draw: 5000) Coordinates: * chain (chain) int64 256B 0 1 2 3 4 5 6 7 8 ... 23 24 25 26 27 28 29 30 31 * draw (draw) int64 40kB 0 1 2 3 4 5 6 ... 4994 4995 4996 4997 4998 4999 Data variables: lp (chain, draw) float64 1MB -9.589e+04 -9.589e+04 ... -54.32 -54.32 Attributes: created_at: 2025-04-17T16:36:22.409477+00:00 arviz_version: 0.21.0 inference_library: emcee inference_library_version: 3.1.6 -
<xarray.Dataset> Size: 2kB Dimensions: (arg_0_dim_0: 50, arg_1_dim_0: 50, arg_2_dim_0: 50) Coordinates: * arg_0_dim_0 (arg_0_dim_0) int64 400B 0 1 2 3 4 5 6 ... 43 44 45 46 47 48 49 * arg_1_dim_0 (arg_1_dim_0) int64 400B 0 1 2 3 4 5 6 ... 43 44 45 46 47 48 49 * arg_2_dim_0 (arg_2_dim_0) int64 400B 0 1 2 3 4 5 6 ... 43 44 45 46 47 48 49 Data variables: arg_0 (arg_0_dim_0) float64 400B 0.1032 0.608 0.6202 ... 9.892 9.906 arg_1 (arg_1_dim_0) float64 400B 4.933 2.136 13.14 ... 274.4 279.4 arg_2 (arg_2_dim_0) float64 400B 1.674 5.671 4.402 ... 2.336 2.816 Attributes: created_at: 2025-04-17T16:36:22.410300+00:00 arviz_version: 0.21.0 inference_library: emcee inference_library_version: 3.1.6
20.4. PyMC#
Note, you need python 3.11 and not newer!
Instalation - https://www.pymc.io/projects/docs/en/latest/installation.html Simple linear regression - https://www.pymc.io/projects/docs/en/stable/learn/core_notebooks/GLM_linear.html#glm-linear
import pymc as pm
# model is y = c0 + c1*x + c2*x^2 + noise
# build a model via a `with` context block.
with pm.Model() as model:
# define priors on polynomial coeffiencts and the added noise
c0 = pm.Normal('c0', 0, 20)
c1 = pm.Normal('c1', 0, 20)
c2 = pm.Normal('c2', 0, 20)
noise = pm.Exponential('noise', 0.1) #could be half-Normal or half-chauchy
# define observations: y = c0 + c1*x + c2*x^2
# link variables to data with `observed=y`
obs = pm.Normal('obs', c0 + c1*x + c2*x**2, noise, observed=y)
# run sampler
idata = pm.sample()
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [c0, c1, c2, noise]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 2 seconds.
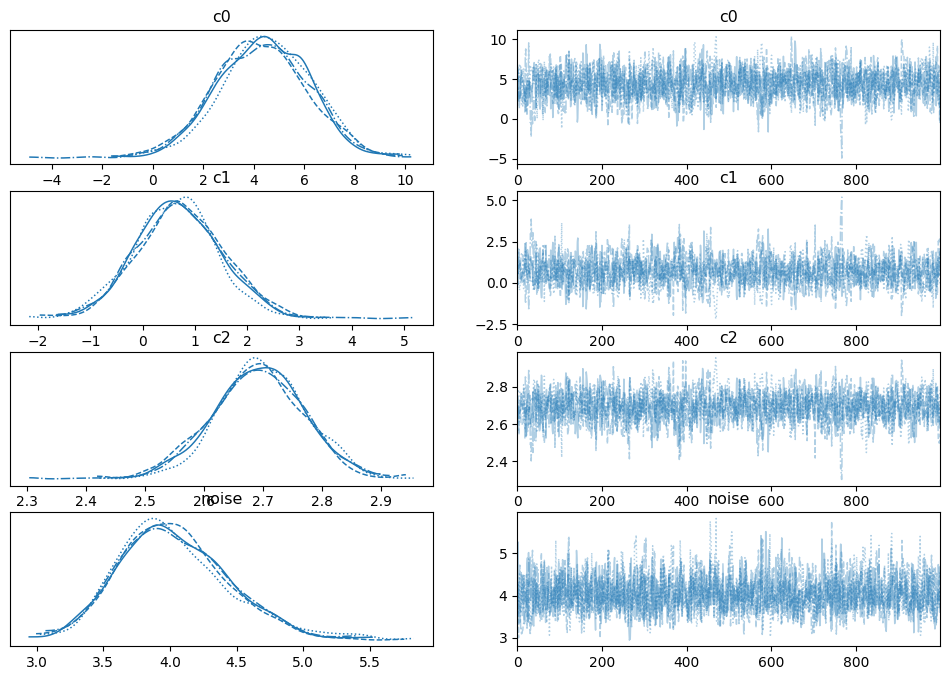
az.plot_trace(idata)
idata
arviz.InferenceData
-
<xarray.Dataset> Size: 136kB Dimensions: (chain: 4, draw: 1000) Coordinates: * chain (chain) int64 32B 0 1 2 3 * draw (draw) int64 8kB 0 1 2 3 4 5 6 7 ... 993 994 995 996 997 998 999 Data variables: c0 (chain, draw) float64 32kB 1.513 5.171 6.126 ... 6.474 -0.265 1.946 c1 (chain, draw) float64 32kB 1.467 0.9078 0.5758 ... 0.3951 2.058 1.9 c2 (chain, draw) float64 32kB 2.64 2.629 2.656 ... 2.689 2.622 2.594 noise (chain, draw) float64 32kB 4.546 4.849 5.271 ... 4.319 4.681 3.903 Attributes: created_at: 2025-04-17T16:36:26.038529+00:00 arviz_version: 0.21.0 inference_library: pymc inference_library_version: 5.22.0 sampling_time: 1.728687047958374 tuning_steps: 1000 -
<xarray.Dataset> Size: 496kB Dimensions: (chain: 4, draw: 1000) Coordinates: * chain (chain) int64 32B 0 1 2 3 * draw (draw) int64 8kB 0 1 2 3 4 5 ... 995 996 997 998 999 Data variables: (12/17) energy (chain, draw) float64 32kB 155.8 157.0 ... 158.7 max_energy_error (chain, draw) float64 32kB -0.1853 1.758 ... -1.049 n_steps (chain, draw) float64 32kB 15.0 31.0 ... 31.0 31.0 step_size_bar (chain, draw) float64 32kB 0.133 0.133 ... 0.1121 step_size (chain, draw) float64 32kB 0.105 0.105 ... 0.1153 process_time_diff (chain, draw) float64 32kB 0.00036 ... 0.000682 ... ... reached_max_treedepth (chain, draw) bool 4kB False False ... False False energy_error (chain, draw) float64 32kB -0.1607 0.5268 ... -0.525 perf_counter_start (chain, draw) float64 32kB 7.477e+04 ... 7.478e+04 acceptance_rate (chain, draw) float64 32kB 0.98 0.683 ... 0.9755 smallest_eigval (chain, draw) float64 32kB nan nan nan ... nan nan largest_eigval (chain, draw) float64 32kB nan nan nan ... nan nan Attributes: created_at: 2025-04-17T16:36:26.048798+00:00 arviz_version: 0.21.0 inference_library: pymc inference_library_version: 5.22.0 sampling_time: 1.728687047958374 tuning_steps: 1000 -
<xarray.Dataset> Size: 800B Dimensions: (obs_dim_0: 50) Coordinates: * obs_dim_0 (obs_dim_0) int64 400B 0 1 2 3 4 5 6 7 ... 43 44 45 46 47 48 49 Data variables: obs (obs_dim_0) float64 400B 4.933 2.136 13.14 ... 263.7 274.4 279.4 Attributes: created_at: 2025-04-17T16:36:26.051738+00:00 arviz_version: 0.21.0 inference_library: pymc inference_library_version: 5.22.0
You might need to install Graphviz, https://graphviz.org/download/
pm.model_to_graphviz(model)
with model:
idata.extend(pm.sample_prior_predictive())
idata.extend(pm.sample_posterior_predictive(idata))
Sampling: [c0, c1, c2, noise, obs]
Sampling: [obs]
idata
arviz.InferenceData
-
<xarray.Dataset> Size: 136kB Dimensions: (chain: 4, draw: 1000) Coordinates: * chain (chain) int64 32B 0 1 2 3 * draw (draw) int64 8kB 0 1 2 3 4 5 6 7 ... 993 994 995 996 997 998 999 Data variables: c0 (chain, draw) float64 32kB 1.513 5.171 6.126 ... 6.474 -0.265 1.946 c1 (chain, draw) float64 32kB 1.467 0.9078 0.5758 ... 0.3951 2.058 1.9 c2 (chain, draw) float64 32kB 2.64 2.629 2.656 ... 2.689 2.622 2.594 noise (chain, draw) float64 32kB 4.546 4.849 5.271 ... 4.319 4.681 3.903 Attributes: created_at: 2025-04-17T16:36:26.038529+00:00 arviz_version: 0.21.0 inference_library: pymc inference_library_version: 5.22.0 sampling_time: 1.728687047958374 tuning_steps: 1000 -
<xarray.Dataset> Size: 2MB Dimensions: (chain: 4, draw: 1000, obs_dim_0: 50) Coordinates: * chain (chain) int64 32B 0 1 2 3 * draw (draw) int64 8kB 0 1 2 3 4 5 6 7 ... 993 994 995 996 997 998 999 * obs_dim_0 (obs_dim_0) int64 400B 0 1 2 3 4 5 6 7 ... 43 44 45 46 47 48 49 Data variables: obs (chain, draw, obs_dim_0) float64 2MB -6.039 5.396 ... 276.8 274.3 Attributes: created_at: 2025-04-17T16:36:26.984700+00:00 arviz_version: 0.21.0 inference_library: pymc inference_library_version: 5.22.0 -
<xarray.Dataset> Size: 496kB Dimensions: (chain: 4, draw: 1000) Coordinates: * chain (chain) int64 32B 0 1 2 3 * draw (draw) int64 8kB 0 1 2 3 4 5 ... 995 996 997 998 999 Data variables: (12/17) energy (chain, draw) float64 32kB 155.8 157.0 ... 158.7 max_energy_error (chain, draw) float64 32kB -0.1853 1.758 ... -1.049 n_steps (chain, draw) float64 32kB 15.0 31.0 ... 31.0 31.0 step_size_bar (chain, draw) float64 32kB 0.133 0.133 ... 0.1121 step_size (chain, draw) float64 32kB 0.105 0.105 ... 0.1153 process_time_diff (chain, draw) float64 32kB 0.00036 ... 0.000682 ... ... reached_max_treedepth (chain, draw) bool 4kB False False ... False False energy_error (chain, draw) float64 32kB -0.1607 0.5268 ... -0.525 perf_counter_start (chain, draw) float64 32kB 7.477e+04 ... 7.478e+04 acceptance_rate (chain, draw) float64 32kB 0.98 0.683 ... 0.9755 smallest_eigval (chain, draw) float64 32kB nan nan nan ... nan nan largest_eigval (chain, draw) float64 32kB nan nan nan ... nan nan Attributes: created_at: 2025-04-17T16:36:26.048798+00:00 arviz_version: 0.21.0 inference_library: pymc inference_library_version: 5.22.0 sampling_time: 1.728687047958374 tuning_steps: 1000 -
<xarray.Dataset> Size: 20kB Dimensions: (chain: 1, draw: 500) Coordinates: * chain (chain) int64 8B 0 * draw (draw) int64 4kB 0 1 2 3 4 5 6 7 ... 493 494 495 496 497 498 499 Data variables: noise (chain, draw) float64 4kB 15.29 25.83 38.63 ... 19.04 0.5792 25.79 c0 (chain, draw) float64 4kB 23.65 6.202 -15.69 ... 7.555 -2.843 c1 (chain, draw) float64 4kB 10.96 -24.31 -10.84 ... -12.55 18.85 c2 (chain, draw) float64 4kB 40.59 19.4 26.69 ... -25.37 -11.07 11.33 Attributes: created_at: 2025-04-17T16:36:26.868724+00:00 arviz_version: 0.21.0 inference_library: pymc inference_library_version: 5.22.0 -
<xarray.Dataset> Size: 204kB Dimensions: (chain: 1, draw: 500, obs_dim_0: 50) Coordinates: * chain (chain) int64 8B 0 * draw (draw) int64 4kB 0 1 2 3 4 5 6 7 ... 493 494 495 496 497 498 499 * obs_dim_0 (obs_dim_0) int64 400B 0 1 2 3 4 5 6 7 ... 43 44 45 46 47 48 49 Data variables: obs (chain, draw, obs_dim_0) float64 200kB 9.356 39.27 ... 1.317e+03 Attributes: created_at: 2025-04-17T16:36:26.871709+00:00 arviz_version: 0.21.0 inference_library: pymc inference_library_version: 5.22.0 -
<xarray.Dataset> Size: 800B Dimensions: (obs_dim_0: 50) Coordinates: * obs_dim_0 (obs_dim_0) int64 400B 0 1 2 3 4 5 6 7 ... 43 44 45 46 47 48 49 Data variables: obs (obs_dim_0) float64 400B 4.933 2.136 13.14 ... 263.7 274.4 279.4 Attributes: created_at: 2025-04-17T16:36:26.051738+00:00 arviz_version: 0.21.0 inference_library: pymc inference_library_version: 5.22.0
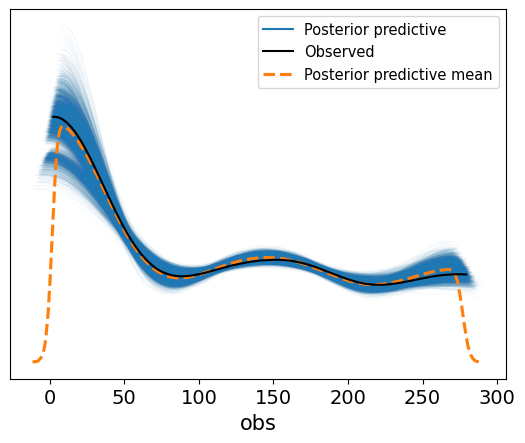
az.plot_ppc(idata, alpha=0.03, textsize=14)
<Axes: xlabel='obs'>
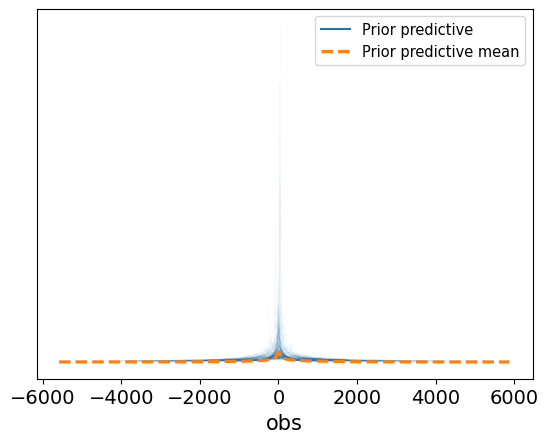
az.plot_ppc(idata, alpha=0.03, textsize=14, group="prior")
<Axes: xlabel='obs'>
20.5. Further Reading#
Inference Data - https://python.arviz.org/en/latest/getting_started/XarrayforArviZ.html
PyMC basics - https://www.pymc.io/projects/docs/en/stable/learn/core_notebooks/pymc_overview.html
Simple linear regression - https://www.pymc.io/projects/docs/en/stable/learn/core_notebooks/GLM_linear.html#glm-linear
%load_ext watermark
%watermark -untzvm -iv -w
Last updated: Thu Apr 17 2025 11:36:34CDT
Python implementation: CPython
Python version : 3.11.12
IPython version : 9.1.0
Compiler : Clang 18.1.8
OS : Darwin
Release : 24.4.0
Machine : arm64
Processor : arm
CPU cores : 12
Architecture: 64bit
arviz : 0.21.0
pandas : 2.2.3
matplotlib: 3.10.1
rich : 14.0.0
numpy : 1.25.2
emcee : 3.1.6
pymc : 5.22.0
Watermark: 2.5.0